Самое большое число которое имеет название. Не вошедшее в сборник сочинений
Когда-то в детстве, мы учились считать до десяти, потом до ста, потом до тысячи. Так какое самое большое число вы знаете? Тысяча, миллион, миллиард, триллион... А дальше? Петаллион, скажет кто-то, и будет не прав, ибо путает приставку СИ, с совсем другим понятием.
На самом деле вопрос не так прост, как кажется на первый взгляд. Во-первых мы говорим об именовании названий степеней тысячи. И тут, первый нюанс, который многие знают по американским фильмам - наш миллиард они называют биллионом.
Дальше больше, существует два вида шкал - длинная и короткая. В нашей стране используется короткая шкала. В этой шкале на каждом шаге мантиса увеличивается на три порядка, т.е. умножаем на тысячу - тысяча 10 3 , миллион 10 6 , миллиард/биллион 10 9 , триллион (10 12). В длинной шкале после миллиарда 10 9 идет биллион 10 12 , а в дальнейшем мантиса уже увеличивается на шесть порядков, и следующее число, которое называется триллион, уже обозначает 10 18 .
Но вернемся к нашей родной шкале. Хотите знать, что идет после триллиона? Пожалуста:
10 3 тысяча
10 6 миллион
10 9 миллиард
10 12 триллион
10 15 квадриллион
10 18 квинтиллион
10 21 секстиллион
10 24 септиллион
10 27 октиллион
10 30 нониллион
10 33 дециллион
10 36 ундециллион
10 39 додециллион
10 42 тредециллион
10 45 кваттуордециллион
10 48 квиндециллион
10 51 cедециллион
10 54 септдециллион
10 57 дуодевигинтиллион
10 60 ундевигинтиллион
10 63 вигинтиллион
10 66 анвигинтиллион
10 69 дуовигинтиллион
10 72 тревигинтиллион
10 75 кватторвигинтиллион
10 78 квинвигинтиллион
10 81 сексвигинтиллион
10 84 септемвигинтиллион
10 87 октовигинтиллион
10 90 новемвигинтиллион
10 93 тригинтиллион
10 96 антригинтиллион
На этом числе наша короткая шкала не выдерживает, и в дальшейшем мантиса увеличивается прогрессивно.
10 100 гугол
10 123 квадрагинтиллион
10 153 квинквагинтиллион
10 183 сексагинтиллион
10 213 септуагинтиллион
10 243 октогинтиллион
10 273 нонагинтиллион
10 303 центиллион
10 306 центуниллион
10 309 центдуоллион
10 312 центтриллион
10 315 центквадриллион
10 402 центтретригинтиллион
10 603 дуцентиллион
10 903 трецентиллион
10 1203 квадрингентиллион
10 1503 квингентиллион
10 1803 сесцентиллион
10 2103 септингентиллион
10 2403 окстингентиллион
10 2703 нонгентиллион
10 3003 миллиллион
10 6003 дуомилиаллион
10 9003 тремиллиаллион
10 3000003 милиамилиаиллион
10 6000003 дуомилиамилиаиллион
10 10 100 гуголплекс
10 3×n+3 зиллион
Гугол
(от англ. googol) - число, в десятичной системе счисления изображаемое единицей со 100 нулями:
10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
1938 году американский математик Эдвард Каснер (Edward Kasner, 1878-1955) гулял по парку с двумя своими племянниками и обсуждал с ними большие числа. В ходе разговора зашла речь о числе со ста нулями, у которого не было собственного названия. Один из племянников, девятилетний Милтон Сиротта (Milton Sirotta), предложил назвать это число «гуголом» (googol). В 1940 году Эдвард Кэснер совместно с Джеймсом Ньюманом написал научно-популярную книгу «Математика и воображение» («New Names in Mathematics»), где и рассказал любителям математики о числе гугол.
Термин «гугол» не имеет серьёзного теоретического и практического значения. Каснер предложил его для того, чтобы проиллюстрировать разницу между невообразимо большим числом и бесконечностью, и с этой целью термин иногда используется при обучении математике.
Гуголплекс
(от англ. googolplex) - число, изображаемое единицей с гуголом нулей. Как и гугол, термин «гуголплекс» был придуман американским математиком Эдвардом Каснером (Edward Kasner) и его племянником Милтоном Сироттой (Milton Sirotta).
Число гугол больше числа всех частиц в известной нам части вселенной, которое составляет величину от 1079 до 1081. Таким образом, число гуголплекс, состоящее из (гугол+1) цифр, в классическом «десятичном» виде записать невозможно, даже если всю материю в известной части вселенной превратить в бумагу и чернила или в компьютерное дисковое пространство.
Зиллион (англ. zillion) - общее название для очень больших чисел.
Этот термин не имеет строгого математического определения. В 1996 году Конвей (англ. J. H. Conway) и Гай (англ. R. K. Guy) в своей книге англ. The Book of Numbers определили зиллион n-ой степени как 10 3×n+3 для системы наименования чисел с короткой шкалой.
В названиях арабских чисел каждая цифра принадлежит своему разряду, а каждые три цифры образуют класс. Таким образом, последняя цифра в числе обозначает количество единиц в нем и называется, соответственно, разрядом единиц. Следующая, вторая с конца, цифра обозначает десятки (разряд десятков), и третья с конца цифра указывает на количество сотен в числе – разряд сотен. Дальше разряды точно также по очереди повторяются в каждом классе, обозначая уже единицы, десятки и сотни в классах тысяч, миллионов и так далее. Если число небольшое и в нем нет цифры десятков или сотен, принято принимать их за ноль. Классы группируют цифры в числах по три, нередко в вычислительных приборах или записях между классами ставится точка или пробел, чтобы визуально разделить их. Это сделано для упрощения чтения больших чисел. Каждый класс имеет свое название: первые три цифры – это класс единиц, далее идет класс тысяч, затем миллионов, миллиардов (или биллионов) и так далее.
Поскольку мы пользуемся десятичной системой исчисления, то основная единица измерения количества – это десяток, или 10 1
. Соответственно с увеличением количества цифр в числе, увеличивается и количество десятков 10 2
,10 3
,10 4
и т.д. Зная количество десятков можно легко определить класс и разряд числа, например, 10 16
– это десятки квадриллионов, а 3×10 16
– это три десятка квадриллионов. Разложение чисел на десятичные компоненты происходит следующий образом – каждая цифра выводится в отдельное слагаемое, умножаясь на требуемый коэффициент 10 n
, где n
– положение цифры по счет слева направо.
Например:
253 981=2×10 6 +5×10 5 +3×10 4 +9×10 3 +8×10 2 +1×10 1
Также степень числа 10 используется и в написании десятичных дробей : 10 (-1) – это 0,1 или одна десятая. Аналогичным образом с предыдущим пунктом, можно разложить и десятичное число, n в таком случае будет обозначать положение цифры от запятой справа налево, например: 0,347629= 3×10 (-1) +4×10 (-2) +7×10 (-3) +6×10 (-4) +2×10 (-5) +9×10 (-6)
Названия десятичных чисел. Десятичные числа читаются по последнему разряду цифр после запятой, например 0,325 – триста двадцать пять тысячных, где тысячные – это разряд последней цифры 5 .
Таблица названий больших чисел, разрядов и классов
| 1-й класс единицы |
1-й разряд единицы 2-й разряд десятки 3-й разряд сотни |
1 = 10 0 10 = 10 1 100 = 10 2 |
| 2-й класс тысячи |
1-й разряд единицы тысяч 2-й разряд десятки тысяч 3-й разряд сотни тысяч |
1 000 = 10 3 10 000 = 10 4 100 000 = 10 5 |
| 3-й класс миллионы |
1-й разряд единицы миллионов 2-й разряд десятки миллионов 3-й разряд сотни миллионов |
1 000 000 = 10 6 10 000 000 = 10 7 100 000 000 = 10 8 |
| 4-й класс миллиарды |
1-й разряд единицы миллиардов 2-й разряд десятки миллиардов 3-й разряд сотни миллиардов |
1 000 000 000 = 10 9 10 000 000 000 = 10 10 100 000 000 000 = 10 11 |
| 5-й класс триллионы |
1-й разряд единицы триллионов 2-й разряд десятки триллионов 3-й разряд сотни триллионов |
1 000 000 000 000 = 10 12 10 000 000 000 000 = 10 13 100 000 000 000 000 = 10 14 |
| 6-й класс квадриллионы |
1-й разряд единицы квадриллионов 2-й разряд десятки квадриллионов 3-й разряд десятки квадриллионов |
1 000 000 000 000 000 = 10 15 10 000 000 000 000 000 = 10 16 100 000 000 000 000 000 = 10 17 |
| 7-й класс квинтиллионы |
1-й разряд единицы
квинтиллионов
2-й разряд десятки квинтиллионов 3-й разряд сотни квинтиллионов |
1 000 000 000 000 000 000 = 10 18 10 000 000 000 000 000 000 = 10 19 100 000 000 000 000 000 000 = 10 20 |
| 8-й класс секстиллионы |
1-й разряд единицы секстиллионов 2-й разряд десятки секстиллионов 3-й разряд сотни секстиллионов |
1 000 000 000 000 000 000 000 = 10 21 10 000 000 000 000 000 000 000 = 10 22 1 00 000 000 000 000 000 000 000 = 10 23 |
| 9-й класс септиллионы |
1-й разряд единицы септиллионов 2-й разряд десятки септиллионов 3-й разряд сотни септиллионов |
1 000 000 000 000 000 000 000 000 = 10 24 10 000 000 000 000 000 000 000 000 = 10 25 100 000 000 000 000 000 000 000 000 = 10 26 |
| 10-й класс октиллион |
1-й разряд единицы октиллионов 2-й разряд десятки октиллионов 3-й разряд сотни октиллионов |
1 000 000 000 000 000 000 000 000 000 = 10 27 10 000 000 000 000 000 000 000 000 000 = 10 28 100 000 000 000 000 000 000 000 000 000 = 10 29 |
Когда-то я прочитал один трагический рассказ, где повествуется о чукче, которого полярники научили считать и записывать цифры. Магия чисел настолько поразила его, что он решил записать в подаренной полярниками тетради абсолютно все существующие в мире числа подряд, начиная с единицы. Чукча забрасывает все свои дела, перестаёт общаться даже с собственной женой, не охотится больше на нерпу и тюленей, а всё пишет и пишет в тетрадь числа…. Так проходит год. В конце концов тетрадь заканчивается и чукча понимает, что он смог записать лишь малую часть всех чисел. Он горько плачет и в отчаянии сжигает свою исписанную тетрадку, чтобы вновь начать жить простой жизнью рыболова, не думая больше о таинственной бесконечности чисел…
Не будем повторять подвиг этого чукчи и пытаться найти самое большое число, так как любому числу достаточно всего лишь прибавить единицу, чтобы получить число ещё большее. Зададимся хоть и похожим, но другим вопросом: какое из чисел, имеющих собственное название, наибольшее?
Очевидно, что хотя сами числа бесконечны, собственных названий у них не так уж и много, так как большинство из них довольствуются именами, составленными из чисел меньших. Так, например, числа 1 и 100 имеют собственные названия «единица» и «сто», а название числа 101 уже составное («сто один»). Понятно, что в конечном наборе чисел, которых человечество наградило собственным именем, должно быть какое-то наибольшее число. Но как оно называется и чему оно равно? Давайте же, попробуем в этом разобраться и найдём, в конце концов, это самое большое число!
|
«Короткая» и «длинная» шкала
История современной системы наименования больших чисел ведёт начало с середины XV века, когда в Италии стали пользоваться словами «миллион» (дословно — большая тысяча) для тысячи в квадрате, «бимиллион» для миллиона в квадрате и «тримиллион» для миллиона в кубе. Об этой системе мы знаем благодаря французскому математику Николя Шюке (Nicolas Chuquet , ок. 1450 - ок. 1500): в своём трактате «Наука о числах» (Triparty en la science des nombres, 1484) он развил эту идею, предложив дальше воспользоваться латинскими количественными числительными (см. таблицу), добавляя их к окончанию «-иллион». Так, «бимиллион» у Шюке превратился в биллион, «тримиллионом» в триллион, а миллион в четвёртой степени стал «квадриллионом».
В системе Шюке число 10 9 , находившееся между миллионом и биллионом, не имело собственного названия и называлось просто «тысяча миллионов», аналогично 10 15 называлось «тысяча биллионов», 10 21 — «тысяча триллионов» и т.д. Это было не очень удобно, и в 1549 году французский писатель и учёный Жак Пелетье (Jacques Peletier du Mans, 1517-1582) предложил поименовать такие «промежуточные» числа при помощи тех же латинских префиксов, но окончания «-иллиард». Так, 10 9 стало называться «миллиардом», 10 15 — «биллиардом», 10 21 — «триллиардом» и т.д.
Система Шюке-Пелетье постепенно стала популярна и ей стали пользоваться по всей Европе. Однако в XVII веке возникла неожиданная проблема. Оказалось, что некоторые учёные почему-то стали путаться и называть число 10 9 не «миллиардом» или «тысячей миллионов», а «биллионом». Вскоре эта ошибка быстро распространилась, и возникла парадоксальная ситуация — «биллион» стал одновременно синонимом «миллиарда» (10 9) и «миллиона миллионов» (10 18).
Эта путаница продолжалась достаточно долго и привела к тому, что в США создали свою систему наименования больших чисел. По американской системе названия чисел строятся так же, как в системе Шюке, — латинский префикс и окончание «иллион». Однако величины этих чисел отличаются. Если в системе Шюке названия с окончанием «иллион» получали числа, которые являлись степенями миллиона, то в американской системе окончание «-иллион» получили степени тысячи. То есть тысяча миллионов (1000 3 = 10 9) стала называться «биллионом», 1000 4 (10 12) — «триллионом», 1000 5 (10 15) — «квадриллионом» и т.д.
Старая же система наименования больших чисел продолжала использоваться в консервативной Великобритании и стала во всём мире называться «британской», несмотря на то, что она была придумана французами Шюке и Пелетье. Однако в 1970-х годах Великобритания официально перешла на «американскую систему», что привело к тому, что называть одну систему американской, а другую британской стало как-то странно. В результате, сейчас американскую систему обычно называют «короткой шкалой», а британскую систему или систему Шюке-Пелетье — «длинной шкалой».
Чтобы не запутаться, подведём промежуточный итог:
|
Короткая шкала наименования используется сейчас в США , Великобритании, Канаде , Ирландии , Австралии , Бразилии и Пуэрто-Рико. В России, Дании , Турции и Болгарии также используется короткая шкала, за исключением того, что число 10 9 называется не «биллион», а «миллиард». Длинная же шкала в настоящее время продолжает использоваться в большинстве остальных стран.
Любопытно, что у нас в стране окончательный переход к короткой шкале произошёл лишь во второй половине XX века. Так, например, ещё Яков Исидорович Перельман (1882-1942) в своей «Занимательной арифметике» упоминает параллельное существование в СССР двух шкал. Короткая шкала, согласно Перельману, использовалась в житейском обиходе и финансовых расчётах, а длинная — в научных книгах по астрономии и физике. Однако сейчас использовать в России длинную шкалу неправильно, хотя числа там получаются и большие.
Но вернемся к поиску самого большого числа. После дециллиона названия чисел получаются путём объединения приставок. Так получаются такие числа как ундециллион, дуодециллион, тредециллион, кваттордециллион, квиндециллион, сексдециллион, септемдециллион, октодециллион, новемдециллион и т.д. Однако эти названия нам уже не интересны, так как мы условились найти наибольшее число с собственным несоставным названием.
Если же мы обратимся к латинской грамматике, то обнаружим, что несоставных названий для чисел больше десяти у римлян было всего три: viginti — «двадцать», centum — «сто» и mille — «тысяча». Для чисел больше, чем «тысяча», собственных названий у римлян не имелось. Например, миллион (1 000 000) римляне называли «decies centena milia», то есть «десять раз по сотне тысяч». По правилу Шюке, эти три оставшихся латинских числительных дают нам такие названия для чисел как «вигинтиллион», «центиллион» и «миллеиллион».
Итак, мы выяснили, что по «короткой шкале» максимальное число, которое имеет собственное название и не является составным из меньших чисел — это «миллеиллион» (10 3003). Если бы в России была бы принята «длинная шкала» наименования чисел, то самым большим числом с собственным названием оказался бы «миллеиллиард» (10 6003).
Однако существуют названия и для ещё больших чисел.
Числа вне системы
Некоторые числа имеют собственное название, без какой-либо связи с системой наименования при помощи латинских префиксов. И таких чисел немало. Можно, к примеру, вспомнить число e , число «пи», дюжину, число зверя и пр. Однако так как нас сейчас интересуют большие числа, то рассмотрим лишь те числа с собственным несоставным названием, которые больше миллиона.
До XVII века на Руси применялась собственная система наименования чисел. Десятки тысяч назывались «тьмами», сотни тысяч — «легионами», миллионы — «леодрами», десятки миллионов — «воронами», а сотни миллионов — «колодами». Этот счёт до сотен миллионов назывался «малым счётом», а в некоторых рукописях авторами рассматривался и «великий счёт», в котором употреблялись те же названия для больших чисел, но уже с другим смыслом. Так, «тьма» означала уже не десять тысяч, а тысячу тысяч (10 6), «легион» — тьму тем (10 12); «леодр» — легион легионов (10 24), «ворон» — леодр леодров (10 48). «Колодой» же в великом славянском счёте почему-то называли не «ворон воронов» (10 96), а лишь десять «воронов», то есть 10 49 (см. таблицу).
|
Число 10 100 также имеет собственное название и придумал его девятилетний мальчик. А дело было так. В 1938 году американский математик Эдвард Кэснер (Edward Kasner , 1878-1955) гулял по парку с двумя своими племянниками и обсуждал с ними большие числа. В ходе разговора зашла речь о числе со ста нулями, у которого не было собственного названия. Один из племянников, девятилетний Милтон Сиротта (Milton Sirott), предложил назвать это число «гуголом» (googol). В 1940 году Эдвард Кэснер совместно с Джеймсом Ньюманом написал научно-популярную книгу «Математика и воображение» , где и рассказал любителям математики о числе гугол. Еще более широкую известность гугол получил в конце 1990-х, благодаря названной в честь него поисковой машине Google.
Название для ещё большего числа, чем гугол, возникло в 1950 году благодаря отцу информатики Клоду Шеннону (Claude Elwood Shannon , 1916-2001). В своей статье «Программирование компьютера для игры в шахматы» он попытался оценить количество возможных вариантов шахматной игры. Согласно ему, каждая игра длится в среднем 40 ходов и на каждом ходе игрок делает выбор в среднем из 30 вариантов, что соответствует 900 40 (примерно равное 10 118) вариантам игры. Эта работа стала широко известной, и данное число стало называться «числом Шеннона».
В известном буддийском трактате Джайна-сутры, относящемся к 100 году до н.э., встречается число «асанкхейя» равное 10 140 . Считается, что этому числу равно количество космических циклов, необходимых для обретения нирваны.
Девятилетний Милтон Сиротта вошёл в историю математики не только тем, что придумал число гугол, но и тем, что одновременно с ним предложил ещё одно число — «гуголплекс», которое равно 10 в степени «гугол», то есть единице с гуголом нулей.
Ещё два числа, большие, чем гуголплекс, были предложены южноафриканским математиком Стэнли Скьюзом (Stanley Skewes, 1899-1988) при доказательстве гипотезы Римана. Первое число, которое позже стали называть «первым числом Скьюза», равно e в степени e в степени e в степени 79, то есть e e e 79 = 10 10 8,85.10 33 . Однако «второе число Скьюза» ещё больше и составляет 10 10 10 1000 .
Очевидно, что чем больше в числе степеней в степенях, тем сложнее записывать числа и понимать их значение при чтении. Мало того, возможно придумать такие числа (и они, кстати, уже придуманы), когда степени степеней просто не помещаются на страницу. Да, что на страницу! Они не уместятся даже в книгу размером с всю Вселенную! В таком случае встаёт вопрос как же такие числа записывать. Проблема, к счастью, разрешима, и математики разработали несколько принципов для записи таких чисел. Правда, каждый математик, кто задавался этой проблемой, придумывал свой способ записи, что привело к существованию нескольких не связанных друг с другом способов для записи больших чисел — это нотации Кнута, Конвея, Штейнгауза и др. С некоторыми из них нам сейчас предстоит разобраться.
Иные нотации
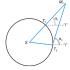
В 1938 году, в тот же год, когда девятилетний Милтон Сиротта придумал числа гугол и гуголплекс, в Польше вышла книжка о занимательной математике «Математический калейдоскоп», написанная Гуго Штейнгаузом (Hugo Dionizy Steinhaus , 1887-1972). Эта книга стала очень популярной, выдержала множество изданий и была переведена на многие языки, в том числе на английский и русский. В ней Штейнгауз, обсуждая большие числа, предлагает простой способ их записи, используя три геометрические фигуры — треугольник, квадрат и круг:
«n
в треугольнике» означает «n n
»,
«n
в квадрате» означает «n
в n
треугольниках»,
«n
в круге» означает «n
в n
квадратах».
Объясняя этот способ записи, Штейнгауз придумывает число «мега», равное 2 в круге и показывает, что оно равно 256 в «квадрате» или 256 в 256 треугольниках. Чтобы подсчитать его, надо 256 возвести в степень 256, получившееся число 3,2.10 616 возвести в степень 3,2.10 616 , затем получившееся число возвести в степень получившегося числа и так далее всего возводить в степень 256 раз. К примеру, калькулятор в MS Windows не может подсчитать из-за переполнения 256 даже в двух треугольниках. Приблизительно же это огромное число составляет 10 10 2.10 619 .
Определив число «мега», Штейнгауз предлагает уже читателям самостоятельно оценить другое число — «медзон», равное 3 в круге. В другом издании книги Штейнгауз вместо медзона предлагает оценить ещё большее число — «мегистон», равное 10 в круге. Вслед за Штейнгаузом я также порекомендую читателям на время оторваться от этого текста и самим попробовать записать эти числа при помощи обычных степеней, чтобы почувствовать их гигантскую величину.
Впрочем, есть названия и для бо льших чисел. Так, канадский математик Лео Мозер (Leo Moser , 1921-1970) доработал нотацию Штейнгауза, которая была ограничена тем, что, если бы потребовалось записать числа много большие мегистона, то возникли бы трудности и неудобства, так как пришлось бы рисовать множество кругов один внутри другого. Мозер предложил после квадратов рисовать не круги, а пятиугольники, затем шестиугольники и так далее. Также он предложил формальную запись для этих многоугольников, чтобы можно было записывать числа, не рисуя сложных рисунков. Нотация Мозера выглядит так:
«n
треугольнике» = n n
= n
;
«n
в квадрате» = n
= «n
в n
треугольниках» = n
n
;
«n
в пятиугольнике» = n
= «n
в n
квадратах» = n
n
;
«n
в k+
1-угольнике» = n
[k
+1] = «n
в n
k
-угольниках» = n
[k
] n
.
Таким образом, по нотации Мозера штейнгаузовский «мега» записывается как 2, «медзон» как 3, а «мегистон» как 10. Кроме того, Лео Мозер предложил называть многоугольник с числом сторон равным меге — «мегагоном». И предложил число «2 в мегагоне», то есть 2. Это число стало известным как число Мозера или просто как «мозер».
Но даже и «мозер» не самое большое число. Итак, самым большим числом, когда-либо применявшимся в математическом доказательстве, является «число Грэма». Впервые это число было использовано американским математиком Рональдом Грэмом (Ronald Graham) в 1977 году при доказательстве одной оценки в теории Рамсея, а именно при подсчёте размерности определённых n -мерных бихроматических гиперкубов. Известность же число Грэма получило лишь после рассказа о нём в вышедшей в 1989 году книге Мартина Гарднера «От мозаик Пенроуза к надёжным шифрам».
Чтобы объяснить, как велико число Грэма, придётся объяснить ещё один способ записи больших чисел, введённый Дональдом Кнутом в 1976 году. Американский профессор Дональд Кнут придумал понятие сверхстепень, которое предложил записывать стрелками, направленными вверх:

Думаю, что всё понятно, поэтому вернёмся к числу Грэма. Рональд Грэм предложил так называемые G-числа:

Вот число G 64 и называется числом Грэма (обозначается оно часто просто как G). Это число является самым большим известным в мире числом, использованным в математическом доказательстве, и занесено даже в «Книгу рекордов Гиннеса».
И напоследок
Написав эту статью, не могу не удержаться от искушения и не придумать своё число. Пусть это число будет называться «стасплекс » и будет равно числу G 100 . Запомните его, и когда ваши дети будут спрашивать, какое самое большое в мире число, говорите им, что это число называется стасплекс .
Новости партнёров
Корректно ответить на этот вопрос нельзя, поскольку числовой ряд не имеет верхнего предела. Так, к любому числу достаточно всего лишь прибавить единицу, чтобы получить число ещё большее. Хотя сами числа бесконечны, собственных названий у них не так уж и много, так как большинство из них довольствуются именами, составленными из чисел меньших. Так, например, числа и имеют собственные названия «единица» и «сто», а название числа уже составное («сто один»). Понятно, что в конечном наборе чисел, которых человечество наградило собственным именем, должно быть какое-то наибольшее число. Но как оно называется и чему оно равно? Давайте же, попробуем в этом разобраться и заодно узнать, насколько большие числа придумали математики.
«Короткая» и «длинная» шкала
История современной системы наименования больших чисел ведёт начало с середины XV века, когда в Италии стали пользоваться словами «миллион» (дословно - большая тысяча) для тысячи в квадрате, «бимиллион» для миллиона в квадрате и «тримиллион» для миллиона в кубе. Об этой системе мы знаем благодаря французскому математику Николя Шюке (Nicolas Chuquet, ок. 1450 – ок. 1500): в своём трактате «Наука о числах» (Triparty en la science des nombres, 1484) он развил эту идею, предложив дальше воспользоваться латинскими количественными числительными (см. таблицу), добавляя их к окончанию «-иллион». Так, «бимиллион» у Шюке превратился в биллион, «тримиллионом» в триллион, а миллион в четвёртой степени стал «квадриллионом».
В системе Шюке число , находившееся между миллионом и биллионом, не имело собственного названия и называлось просто «тысяча миллионов», аналогично называлось «тысяча биллионов», - «тысяча триллионов» и т.д. Это было не очень удобно, и в 1549 году французский писатель и учёный Жак Пелетье (Jacques Peletier du Mans, 1517–1582) предложил поименовать такие «промежуточные» числа при помощи тех же латинских префиксов, но окончания «-иллиард». Так, стало называться «миллиардом», - «биллиардом», - «триллиардом» и т.д.
Система Шюке-Пелетье постепенно стала популярна и ей стали пользоваться по всей Европе. Однако в XVII веке возникла неожиданная проблема. Оказалось, что некоторые учёные почему-то стали путаться и называть число не «миллиардом» или «тысячей миллионов», а «биллионом». Вскоре эта ошибка быстро распространилась, и возникла парадоксальная ситуация - «биллион» стал одновременно синонимом «миллиарда» () и «миллиона миллионов» ().
Эта путаница продолжалась достаточно долго и привела к тому, что в США создали свою систему наименования больших чисел. По американской системе названия чисел строятся так же, как в системе Шюке, - латинский префикс и окончание «иллион». Однако величины этих чисел отличаются. Если в системе Шюке названия с окончанием «иллион» получали числа, которые являлись степенями миллиона, то в американской системе окончание «-иллион» получили степени тысячи. То есть тысяча миллионов () стала называться «биллионом», () - «триллионом», () - «квадриллионом» и т.д.
Старая же система наименования больших чисел продолжала использоваться в консервативной Великобритании и стала во всём мире называться «британской», несмотря на то, что она была придумана французами Шюке и Пелетье. Однако в 1970-х годах Великобритания официально перешла на «американскую систему», что привело к тому, что называть одну систему американской, а другую британской стало как-то странно. В результате, сейчас американскую систему обычно называют «короткой шкалой», а британскую систему или систему Шюке-Пелетье - «длинной шкалой».
Чтобы не запутаться, подведём промежуточный итог:
| Название числа | Значение по «короткой шкале» | Значение по «длинной шкале» |
| Миллион | ||
| Миллиард | ||
| Биллион | ||
| Биллиард | - | |
| Триллион | ||
| Триллиард | - | |
| Квадриллион | ||
| Квадриллиард | - | |
| Квинтиллион | ||
| Квинтиллиард | - | |
| Секстиллион | ||
| Секстиллиард | - | |
| Септиллион | ||
| Септиллиард | - | |
| Октиллион | ||
| Октиллиард | - | |
| Нониллион | ||
| Нониллиард | - | |
| Дециллион | ||
| Дециллиард | - | |
| Вигинтиллион | ||
| Вигинтиллиард | - | |
| Центиллион | ||
| Центиллиард | - | |
| Миллеиллион | ||
| Миллеиллиард | - |
Короткая шкала наименования используется сейчас в США, Великобритании, Канаде, Ирландии, Австралии, Бразилии и Пуэрто-Рико. В России, Дании, Турции и Болгарии также используется короткая шкала, за исключением того, что число называется не «биллион», а «миллиард». Длинная же шкала в настоящее время продолжает использоваться в большинстве остальных стран.
Любопытно, что у нас в стране окончательный переход к короткой шкале произошёл лишь во второй половине XX века. Так, например, ещё Яков Исидорович Перельман (1882–1942) в своей «Занимательной арифметике» упоминает параллельное существование в СССР двух шкал. Короткая шкала, согласно Перельману, использовалась в житейском обиходе и финансовых расчётах, а длинная - в научных книгах по астрономии и физике. Однако сейчас использовать в России длинную шкалу неправильно, хотя числа там получаются и большие.
Но вернемся к поиску самого большого числа. После дециллиона названия чисел получаются путём объединения приставок. Так получаются такие числа как ундециллион, дуодециллион, тредециллион, кваттордециллион, квиндециллион, сексдециллион, септемдециллион, октодециллион, новемдециллион и т.д. Однако эти названия нам уже не интересны, так как мы условились найти наибольшее число с собственным несоставным названием.
Если же мы обратимся к латинской грамматике, то обнаружим, что несоставных названий для чисел больше десяти у римлян было всего три: viginti - «двадцать», centum - «сто» и mille - «тысяча». Для чисел больше, чем «тысяча», собственных названий у римлян не имелось. Например, миллион () римляне называли «decies centena milia», то есть «десять раз по сотне тысяч». По правилу Шюке, эти три оставшихся латинских числительных дают нам такие названия для чисел как «вигинтиллион», «центиллион» и «миллеиллион».
Итак, мы выяснили, что по «короткой шкале» максимальное число, которое имеет собственное название и не является составным из меньших чисел - это «миллеиллион» (). Если бы в России была бы принята «длинная шкала» наименования чисел, то самым большим числом с собственным названием оказался бы «миллеиллиард» ().
Однако существуют названия и для ещё больших чисел.
Числа вне системы
Некоторые числа имеют собственное название, без какой-либо связи с системой наименования при помощи латинских префиксов. И таких чисел немало. Можно, к примеру, вспомнить число e, число «пи», дюжину, число зверя и пр. Однако так как нас сейчас интересуют большие числа, то рассмотрим лишь те числа с собственным несоставным названием, которые больше миллиона.
До XVII века на Руси применялась собственная система наименования чисел. Десятки тысяч назывались «тьмами», сотни тысяч - «легионами», миллионы - «леодрами», десятки миллионов - «воронами», а сотни миллионов - «колодами». Этот счёт до сотен миллионов назывался «малым счётом», а в некоторых рукописях авторами рассматривался и «великий счёт», в котором употреблялись те же названия для больших чисел, но уже с другим смыслом. Так, «тьма» означала уже не десять тысяч, а тысячу тысяч () , «легион» - тьму тем () ; «леодр» - легион легионов () , «ворон» - леодр леодров (). «Колодой» же в великом славянском счёте почему-то называли не «ворон воронов» () , а лишь десять «воронов», то есть (см. таблицу).
| Название числа | Значение в «малом счёте» | Значение в «великом счёте» | Обозначение |
| Тьма | |||
| Легион | |||
| Леодр | |||
| Ворон (вран) | |||
| Колода | |||
| Тьма тем |  |
Число также имеет собственное название и придумал его девятилетний мальчик. А дело было так. В 1938 году американский математик Эдвард Кэснер (Edward Kasner, 1878–1955) гулял по парку с двумя своими племянниками и обсуждал с ними большие числа. В ходе разговора зашла речь о числе со ста нулями, у которого не было собственного названия. Один из племянников, девятилетний Милтон Сиротта (Milton Sirott), предложил назвать это число «гуголом» (googol). В 1940 году Эдвард Кэснер совместно с Джеймсом Ньюманом написал научно-популярную книгу «Математика и воображение», где и рассказал любителям математики о числе гугол. Еще более широкую известность гугол получил в конце 1990-х, благодаря названной в честь него поисковой машине Google.
Название для ещё большего числа, чем гугол, возникло в 1950 году благодаря отцу информатики Клоду Шеннону (Claude Elwood Shannon, 1916–2001). В своей статье «Программирование компьютера для игры в шахматы» он попытался оценить количество возможных вариантов шахматной игры. Согласно ему, каждая игра длится в среднем ходов и на каждом ходе игрок делает выбор в среднем из вариантов, что соответствует (примерно равное ) вариантам игры. Эта работа стала широко известной, и данное число стало называться «числом Шеннона».
В известном буддийском трактате Джайна-сутры, относящемся к 100 году до н.э., встречается число «асанкхейя» равное . Считается, что этому числу равно количество космических циклов, необходимых для обретения нирваны.
Девятилетний Милтон Сиротта вошёл в историю математики не только тем, что придумал число гугол, но и тем, что одновременно с ним предложил ещё одно число - «гуголплекс», которое равно в степени «гугол», то есть единице с гуголом нулей.
Ещё два числа, большие, чем гуголплекс, были предложены южноафриканским математиком Стэнли Скьюзом (Stanley Skewes, 1899–1988) при доказательстве гипотезы Римана. Первое число, которое позже стали называть «первым числом Скьюза», равно в степени в степени в степени , то есть . Однако «второе число Скьюза» ещё больше и составляет .
Очевидно, что чем больше в числе степеней в степенях, тем сложнее записывать числа и понимать их значение при чтении. Мало того, возможно придумать такие числа (и они, кстати, уже придуманы), когда степени степеней просто не помещаются на страницу. Да, что на страницу! Они не уместятся даже в книгу размером с всю Вселенную! В таком случае встаёт вопрос как же такие числа записывать. Проблема, к счастью, разрешима, и математики разработали несколько принципов для записи таких чисел. Правда, каждый математик, кто задавался этой проблемой, придумывал свой способ записи, что привело к существованию нескольких не связанных друг с другом способов для записи больших чисел - это нотации Кнута, Конвея, Штейнгауза и др. С некоторыми из них нам сейчас предстоит разобраться.
Иные нотации
В 1938 году, в тот же год, когда девятилетний Милтон Сиротта придумал числа гугол и гуголплекс, в Польше вышла книжка о занимательной математике «Математический калейдоскоп», написанная Гуго Штейнгаузом (Hugo Dionizy Steinhaus, 1887–1972). Эта книга стала очень популярной, выдержала множество изданий и была переведена на многие языки, в том числе на английский и русский. В ней Штейнгауз, обсуждая большие числа, предлагает простой способ их записи, используя три геометрические фигуры - треугольник, квадрат и круг:
«
в треугольнике» означает «»,
«
в квадрате» означает «
в треугольниках»,
«
в круге» означает «
в квадратах».
Объясняя этот способ записи, Штейнгауз придумывает число «мега», равное в круге и показывает, что оно равно в «квадрате» или в треугольниках. Чтобы подсчитать его, надо возвести в степень , получившееся число возвести в степень , затем получившееся число возвести в степень получившегося числа и так далее всего возводить в степень раз. К примеру, калькулятор в MS Windows не может подсчитать из-за переполнения даже в двух треугольниках. Приблизительно же это огромное число составляет .
Определив число «мега», Штейнгауз предлагает уже читателям самостоятельно оценить другое число - «медзон», равное в круге. В другом издании книги Штейнгауз вместо медзона предлагает оценить ещё большее число - «мегистон», равное в круге. Вслед за Штейнгаузом я также порекомендую читателям на время оторваться от этого текста и самим попробовать записать эти числа при помощи обычных степеней, чтобы почувствовать их гигантскую величину.
Впрочем, есть названия и для больших чисел. Так, канадский математик Лео Мозер (Leo Moser, 1921–1970) доработал нотацию Штейнгауза, которая была ограничена тем, что, если бы потребовалось записать числа много большие мегистона, то возникли бы трудности и неудобства, так как пришлось бы рисовать множество кругов один внутри другого. Мозер предложил после квадратов рисовать не круги, а пятиугольники, затем шестиугольники и так далее. Также он предложил формальную запись для этих многоугольников, чтобы можно было записывать числа, не рисуя сложных рисунков. Нотация Мозера выглядит так:
«
треугольнике» = = ;
«
в квадрате» = = «
в треугольниках» = ;
«
в пятиугольнике» = = «
в квадратах» = ;
«
в -угольнике»
= = «
в -угольниках»
= .
Таким образом, по нотации Мозера штейнгаузовский «мега» записывается как , «медзон» как , а «мегистон» как . Кроме того, Лео Мозер предложил называть многоугольник с числом сторон равным меге - «мегагоном». И предложил число « в мегагоне», то есть . Это число стало известным как число Мозера или просто как «мозер».
Но даже и «мозер» не самое большое число. Итак, самым большим числом, когда-либо применявшимся в математическом доказательстве, является «число Грэма». Впервые это число было использовано американским математиком Рональдом Грэмом (Ronald Graham) в 1977 году при доказательстве одной оценки в теории Рамсея, а именно при подсчёте размерности определённых -мерных бихроматических гиперкубов. Известность же число Грэма получило лишь после рассказа о нём в вышедшей в 1989 году книге Мартина Гарднера «От мозаик Пенроуза к надёжным шифрам».
Чтобы объяснить, как велико число Грэма, придётся объяснить ещё один способ записи больших чисел, введённый Дональдом Кнутом в 1976 году. Американский профессор Дональд Кнут придумал понятие сверхстепень, которое предложил записывать стрелками, направленными вверх.
Обычные арифметические операции - сложение, умножение и возведение в степень - естественным образом могут быть расширены в последовательность гипероператоров следующим образом.
Умножение натуральных чисел может быть определено через повторно производимую операцию сложения («сложить копий числа »):
Например,
Возведение числа в степень может быть определено как повторно производимая операция умножения («перемножить копий числа »), и в обозначениях Кнута эта запись выглядит как одиночная стрелочка, указывающая вверх:
Например,
Такая одиночная стрелка вверх использовалась в качестве значка степени в языке программирования Алгол.
Например,
Здесь и далее вычисление выражения всегда идёт справа налево, также и стрелочные операторы Кнута (как и операция возведение в степень) по определению обладают правой ассоциативностью (очерёдностью справа налево). Согласно данному определению,
Уже это приводит к довольно большим числам, но система обозначений на этом не заканчивается. Оператор «тройная стрелочка» используется для записи повторного возведения в степень оператора «двойная стрелочка» (также известного как «пентация»):
Затем оператора «четверная стрелочка»:
И т. д. Общее правило оператор «-я стрелочка», в соответствии с правой ассоциативностью, продолжается вправо в последовательную серию операторов « стрелочка». Символически это можно записать следующим образом,
Например:
Форма обозначения обычно используется для записи с стрелочками.
Некоторые числа настолько большие, что даже запись стрелочками Кнута становится слишком громоздкой; в этом случае использование оператора -стрелочка предпочтительней (и также для описания с изменяемым числом стрелочек), или эквивалентно, гипероператорам. Но некоторые числа настолько огромны, что даже подобная запись недостаточна. Например, число Грэма.
При использовании Стрелочной нотации Кнута число Грэма может быть записано как
Где количество стрелок в каждом слое, начиная с верхнего, определяется числом в следующем слое, то есть , где , где верхний индекс у стрелки показывает общее количество стрелок. Другими словами, вычисляется в шага: на первом шаге мы вычисляем с четырьмя стрелками между тройками, на втором - с стрелками между тройками, на третьем - с стрелками между тройками и так далее; в конце мы вычисляем с стрелок между тройками.
Это может быть записано как , где , где верхний индекс у означает итерации функций.
Если другим числам с «именами» можно подобрать соответствующее число объектов (например, количество звезд в видимой части Вселенной оценивается в секстильонов - , а количество атомов, из которых состоит земной шар имеет порядок додекальонов), то гугол уже «виртуальный», не говоря уже об числе Грэма. Масштаб только первого члена настолько велик, что его практически невозможно осознать, хотя запись выше относительно проста для понимания. Хотя - это всего лишь количество башен в этой формуле для , уже это число много больше количества объёмов Планка (наименьший возможный физический объём), которые содержатся в наблюдаемой вселенной (примерно ). После первого члена нас ожидают ещё члена стремительно растущей последовательности.
Вопрос "Какое самое большое число в мире?", по меньшей мере, некорректен. Существуют как различные системы исчислений – десятичная, двоичная и шестнадцатеричная, так и разнообразные категории чисел – полупростые и простые, причем последние делятся на законные и незаконные. Кроме того, есть числа Скьюза (Skewes" number), Стейнхауза и других математиков, которые то ли в шутку, то ли всерьез изобретают и выкладывают на суд публики такие экзоты, как «мегистон» или «мозер».
Какое самое большое число в мире в десятичной системе
Из десятичной системы большинству «нематематиков» хорошо известны миллион, миллиард и триллион. Причем, если миллион у россиян, в основном, ассоциируется с долларовой взяткой, которую можно унести в чемоданчике, то куда распихать миллиард (не говоря уже о триллионе) североамериканских денежных знаков - у большинства не хватает фантазии. Однако в теории больших чисел существуют такие понятия, как квадриллион (десять в пятнадцатой степени – 1015), секстиллион (1021) и октиллион (1027).

В английской, наиболее широко распространенной в мире десятичной системе максимальным числом считается дециллион - 1033.
В 1938 году, в связи с развитием прикладной математики и расширением микро- и макромира, профессор Колумбийского университета (США), Эдвард Каснер (Edward Kasner) опубликовал на страницах журнала «Scripta Mathematica» предложение своего девятилетнего племянника использовать в десятичной системе исчисления в качестве самого большого числа «гугол» («googol») – представляющее собой десять в сотой степени (10100), который на бумаге выражается как единица со ста нулями. Однако они не остановились на этом и через несколько лет предложили ввести в обращение новое самое большое число в мире – «гуголплекс» (googolplex), которое представляет собой десять, возведенное в десятую степень и еще раз возведенное в сотую степень – (1010)100, выражаемое единицей, к которой справа приписан гугол нулей. Впрочем, для большинства даже профессиональных математиков и «гугол», и «гуголплекс» представляют чисто умозрительный интерес, и вряд ли в повседневной практике их можно к чему-либо применить.
Экзотические числа
Какое самое большое число в мире среди простых чисел – тех, которые могут делиться только на самих себя и на единицу. Одним из первых, кто зафиксировал самое большое простое число, равное 2 147 483 647, был великий математик Леонард Эйлер. На январь 2016 года, таким числом признано выражение, вычисляемое как 274 207 281 – 1.